Define Simetría En Un Plano Cartesiano

Simetría en el plano cartesiano.
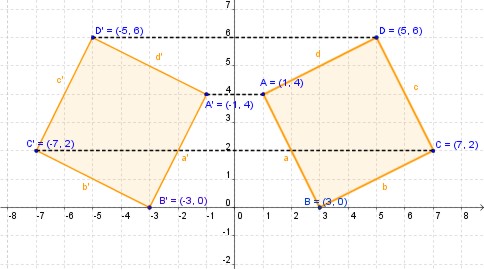
Define simetría en un plano cartesiano. Al comparar las coordenadas de los vértices de ambos triángulos y el vector traslación nos podemos dar cuenta de lo siguiente. Por lo tanto podemos concluir que para trasladar un polígono en el plano a este se le deben sumar las coordenadas de sus vértices con las del vector para obtener las coordenadas del polígono trasladado. En este caso el eje de simetría es una recta vertical. Para obtener una simetria en el plano cartesiano se debe considerar lo siguiente.
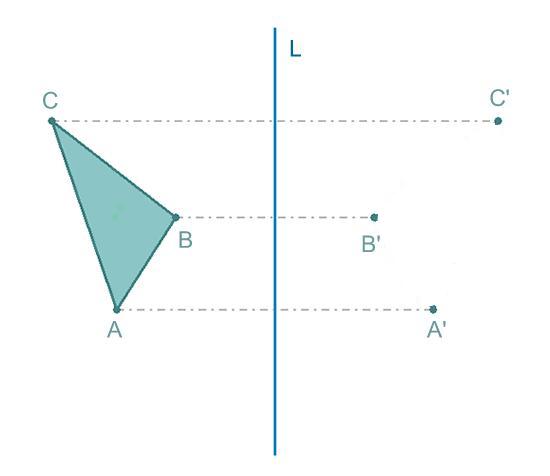
En la figura siguiente se muestra un ejemplo de simetría axial. Simetrias en elementos cotideanos. Las rectas a a b b c c y d d son ahora perpendiculares al eje de simetría y la distancia desde a al eje coincide con la distancia del punto transformado a al eje. El plano cartesiano simetria axial traslaciones del plano carteciano una simeria axial es un desplasamiento que intercambia los puntos de los dos lados de determinada recta llamada eje simetria.
A instancias de las matemáticas el plano cartesiano es un sistema de referencias que se encuentra conformado por dos rectas numéricas una horizontal y otra vertical que se cortan en un determinado punto. Enlaces a sitios de mis colegas. Se define a la simetría axial como una transformación isométrica en el plano respecto de un eje de simetría en la cual cada punto de la figura en cuestión se corresponde con otro punto de plano llamado imagen que se halla respetando las dos siguientes condiciones. En este caso el eje de simetría es una recta vertical.
A la horizontal se la llama eje de las abscisas o de las x y al vertical eje de las coordenadas o de las yes en tanto el punto en el cual se cortarán se denomina origen. Presentación clase de simetria. Breve explicación de cómo realizar la reflexión de una figura geométrica en el plano cartesiano conociendo los puntos vértices que la componen dentro del.